1. 함수 나타내기
다항함수 방정식을 코드를 통해 그려보는 방법을 알아보겠습니다.

그림 그리는 데이터는 numpy로, matplotlib로 그려보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
x의 변화에 대한 y의 변화를 그리는 것인데, 다항식만 쓰기엔 x값이 없습니다. 이럴 땐 x값부터 정해주어야 합니다.
x는 -3부터 2까지 100개의 데이터를 만든다고 생각하면 됩니다. 따라서 numpy의 linspace를 이용합니다.
x = np.linspace(-3, 2, 100)
y = 3 * x**2 + 2
x를 출력해보겠습니다.
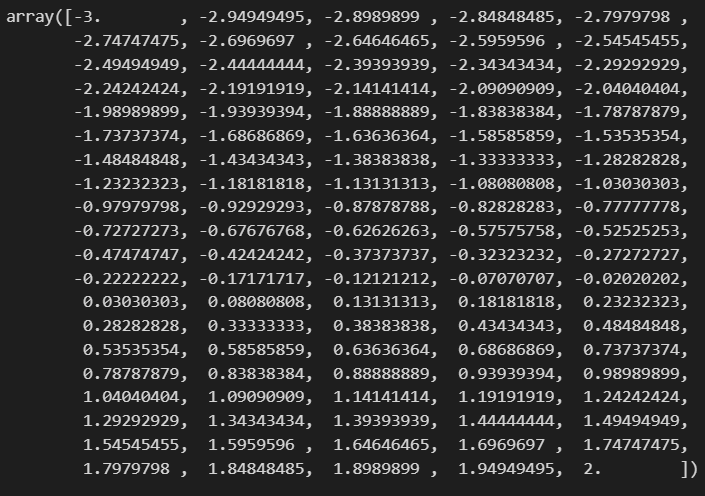
함수 식에 따라 y도 정의되었으니 y도 출력해보겠습니다.

이걸 토대로 그래프를 그릴 수 있습니다.
그래프는 pyplot의 plot함수를 사용합니다.
plt.figure(figsize=(12,8))
plt.plot(x, y)
plt.show()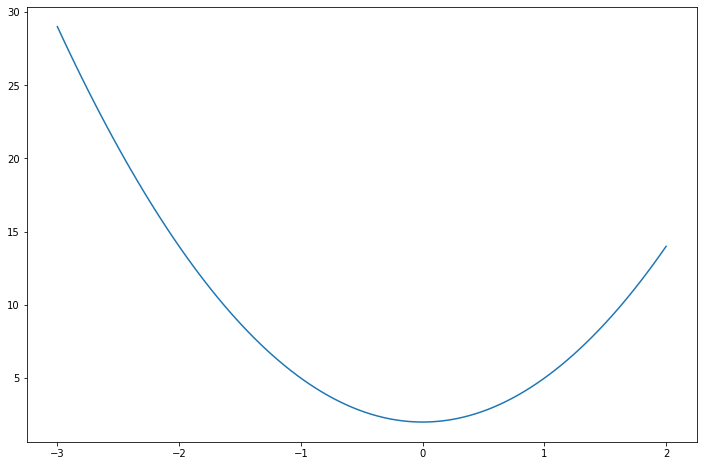
여기에 몇개의 장치를 추가해보겠습니다. grid를 넣고 x,y 축에 label을 넣어보겠습니다.
plt.figure(figsize=(12,8))
plt.plot(x, y)
#여기에 몇개의 장치를 추가해보겠습니다.
plt.grid()
plt.xlabel('$x$') #$기호로 감싸주면 수학기호를 추가할 수 있습니다.
plt.ylabel('$3x^2+2$')
plt.show()
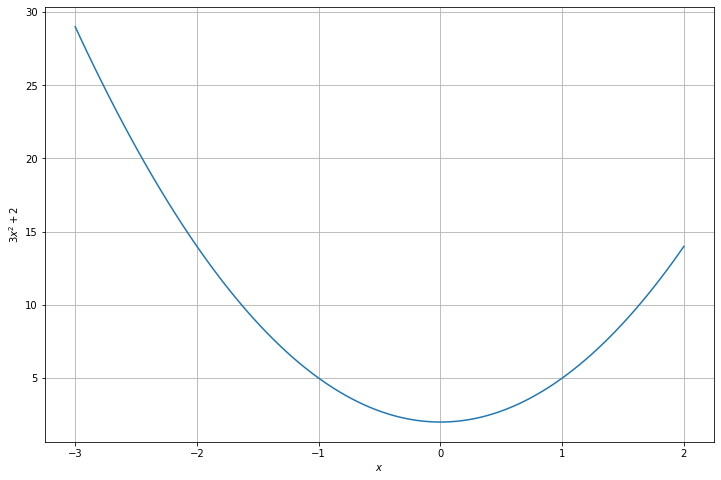
matplotlib에서 제공하는 style로 grid를 써볼 수도 있습니다.
import matplotlib as mpl
#matplotlib에서 제공하는 style로 grid를 써볼 수도 있습니다.
mpl.style.use('seaborn-whitegrid')
plt.figure(figsize=(12,8))
plt.plot(x, y)
plt.xlabel('$x$')
plt.ylabel('$3x^2+2$')
plt.show()
fontsize를 키우는 법도 있습니다.
#font size를 키우기
import matplotlib as mpl
mpl.style.use('seaborn-whitegrid')
plt.figure(figsize=(12,8))
plt.plot(x, y)
plt.xlabel('$x$', fontsize=25)
plt.ylabel('$3x^2+2$', fontsize=25)
plt.show()
2. 다항함수의 x축방향 이동
x축 방향으로 이동하면 x자리에 x+1을 넣으면 x축 방향으로 -1만큼 간겁니다.
x = np.linspace(-5, 5, 100)
y1 = 3 * x**2 + 2
y2 = 3 * (x+1)**2 + 2 #y2는 x자리에 x+1를 넣은 함수plt.figure(figsize=(12,8))
plt.plot(x, y1, lw=2, ls='dashed', label='$y=3x^2 +2$')
plt.plot(x, y2, label='$y=3(x+1)^2 +2$')
plt.legend(fontsize=15)
plt.xlabel('$x$', fontsize=25)
plt.ylabel('$3x^2+2$', fontsize=25)
plt.show()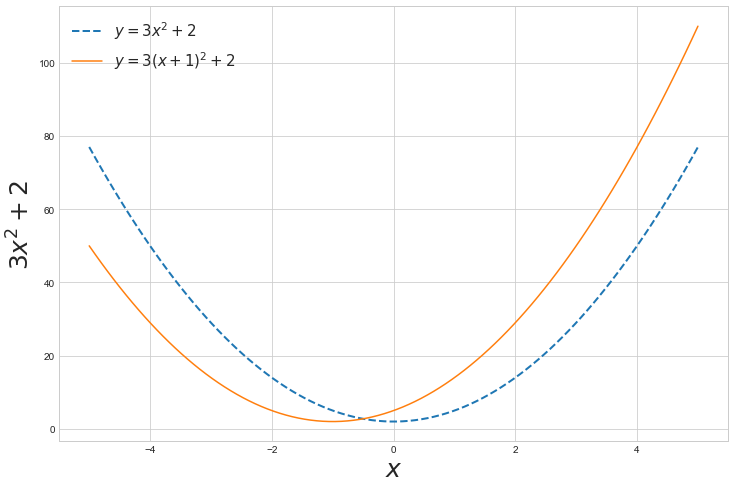
0기준으로 그려진 그래프가 -1만큼 이동해서 다시 그려지는 걸 볼 수 있습니다.
3. 지수함수
지수함수를 파악하기 위해 다양한 경우를 보겠습니다.

x = np.linspace(-2, 2, 100)
a11, a12, a13 = 2, 3, 4
y11, y12, y13 = a11**x, a12**x, a13**x
a21, a22, a23 = 1/2, 1/3, 1/4
y21, y22, y23 = a21**x, a22**x, a23**x
각 그래프를 한 그래프에서 비교해보겠습니다.
fig, ax = plt.subplots(1, 2, figsize=(12, 6)) #1행 2열로 subplots를 그려라.
두개를 그리라고 했기 때문에 ax가 2개가 나옵니다.
실제로 len(ax) 코드를 실행시키면 2가 출력됩니다.
그래프를 그려보겠습니다.
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
ax[0].plot(x, y11, color='k', label='$2^x$')
ax[0].plot(x, y12, '--', color='k', label='$3^x$')
ax[0].plot(x, y13, ':', color='k', label='$4^x$')
ax[0].legend(fontsize=20)
ax[1].plot(x, y21, color='k', label='$(1/2)^x$')
ax[1].plot(x, y22, '--', color='k', label='$(1/3)^x$')
ax[1].plot(x, y23, ':', color='k', label='$(1/4)^x$')
ax[1].legend(fontsize=20)
plt.show()
2^x와 (1/2)^x는 비교하면, 2^x와 2^(-x)로도 볼 수 있습니다. x에 -가 붙는다는건 y축대칭이 되기 때문에 위와같은 그래프가 나오는게 맞습니다.
지수증가
x = np.linspace(0, 10)
plt.figure(figsize=(6,6))
plt.plot(x, x**2, '--', color='k', label='$x^2$')
plt.plot(x, 2**x, color='k', label='$2^x$')
plt.show()
4. 특이한 지수함수

변수가 두 군데 존재하는 지수식이 있습니다.
x = np.array([10, 100, 1000, 10000, 100000, 1000000, 10000000])
y = (1 + 1/x)**x
y
값을 보면 점점 수렴하는 걸 볼 수 있습니다.
이것이 바로 자연상수 e인데요, 베르누이가 2.7182818... 이라는 숫자가 있다는 것을 밝히고 오일러가 자연상수 e라는 표기를 시작했습니다.
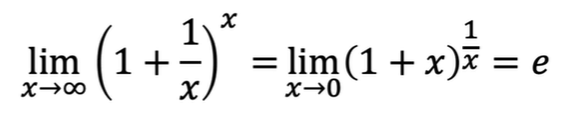
2의 몇승을 하면 16이 될까?를 생각해서 log도 등장하게 되었습니다.
우선 자연상수 e함수와, 로그 함수를 그려보겠습니다.
np.exp(1)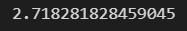
np.log(np.exp(1))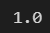
log 밑수를 base라고 두고 윗수를 x라고 하면 이는 log(a)/log(base)가 되는 식을 이용하겠습니다.
def log(x, base):
return np.log(x)/np.log(base)
x1 = np.linspace(0.0001, 5, 1000)
x2 = np.linspace(0.01, 5, 100)
y11, y12 = log(x1, 10), log(x2, np.e)
y21, y22 = log(x1, 1/10), log(x2, (1/np.e))
그래프로 그려보겠습니다.
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
ax[0].plot(x1, y11, label='$\log_{10} x$', color='k')
ax[0].plot(x2, y12, '--', label='$\log_{e} x$', color='k')
ax[0].set_xlabel('$x$', fontsize=25)
ax[0].set_ylabel('$y$', fontsize=25)
ax[0].legend(fontsize=20, loc='lower right')
ax[1].plot(x1, y21, label='$\log_{1/10} x$', color='k')
ax[1].plot(x2, y22, '--', label='$\log_{1/e} x$', color='k')
ax[1].set_xlabel('$x$', fontsize=25)
ax[1].set_ylabel('$y$', fontsize=25)
ax[1].legend(fontsize=20, loc='upper right')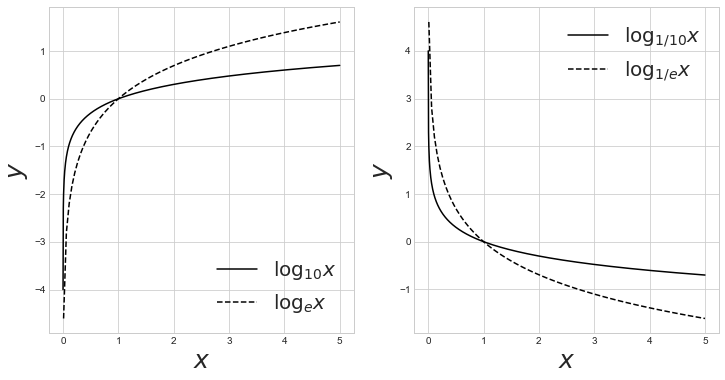
5. 시그모이드
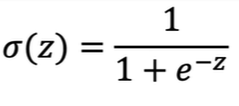
시그모이드 함수는 S자형 곡선 또는 시그모이드 곡선을 갖는 수학 함수이다. 시그모이드 함수의 예시로는 로지스틱 함수가 있습니다.
로지스틱 회귀에서는 활성화 함수를 시그모이드 함수를 사용하는데,
시그모이드 함수는 z를 0~1 사이의 확률값으로 변환시켜 주는 확률로 해석 할 수 있습니다.
z = np.linspace(-10,10,100)
sigma = 1/(1+np.exp(-z))
plt.figure(figsize=(12,8))
plt.plot(z, sigma)
plt.show()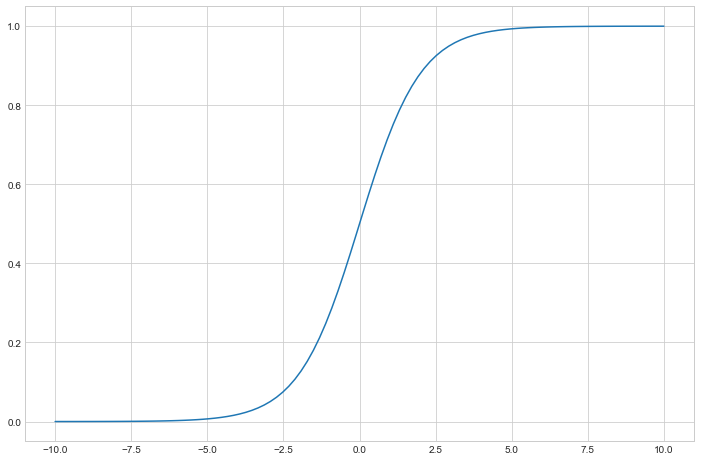
plt.figure(figsize=(12,8))
plt.plot(z, sigma)
plt.xlabel('$z$', fontsize=25)
plt.ylabel('$\sigma(z)$', fontsize=25)
plt.show()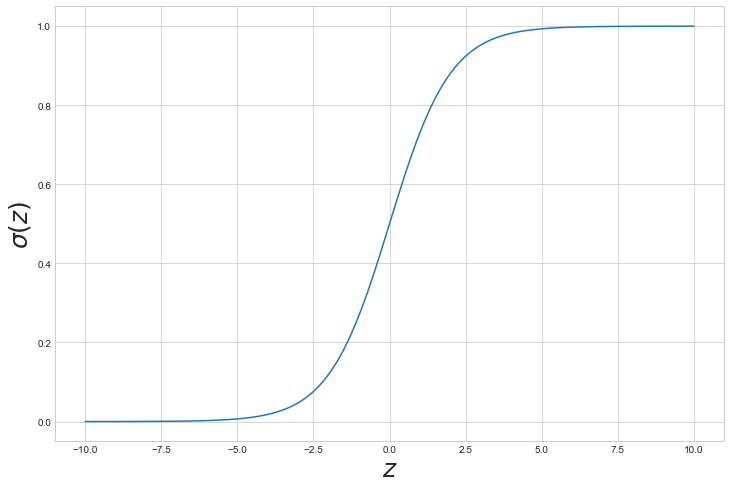
시그모이드는 0과 1 사이의 값을 갖는다는걸 꼭 기억해야합니다.
6. 벡터의 표현
열벡터 행벡터
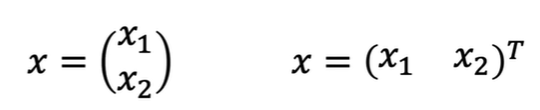
단일변수 스칼라함수

다중변수 스칼라함수
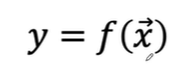
x에 벡터표시가 있으면, x가 여러개의 값을 가졌다는 것을 의미합니다. 열벡터의 값을 가졌다고 보면 됩니다. 그래서 이름이 다중변수입니다. 다중변수에 출력이 하나라서 다중변수 스칼라함수입니다.
다변수 벡터함수

들어가는 x입력이 벡터입니다. 출력이 열로 나오는겁니다. 이러면 벡터함수입니다.
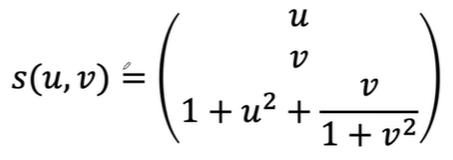
다변수 벡터함수의 예제하나
u와 v를 받아서 u, v, 1+~~~ 인 세개가 출력되는 함수입니다.
이 함수를 그려보겠습니다.
numpy가 제공하는 meshgrid라는 함수를 자주 쓰기 때문에 사용법을 헷갈릴 수 있어 주의해야합니다.
u = np.linspace(0, 5, 6)
v = np.linspace(0, 5, 6)
v
U, V = np.meshgrid(u, v)
UU : 열 방향으로 나열
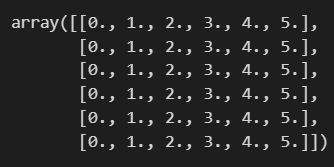
V : 행 방향으로 나열

u = np.linspace(0, 1, 30)
v = np.linspace(0, 1, 30)
U, V = np.meshgrid(u, v)
U + V
X = U
Y = V
Z = (1 + U**2) + V / (1 + V**2)
Z
그래프로 그려보겠습니다.
u와 v가 입력되고 출력이 Z므로 3차원상에서 둥실둥실 떠있는 그래프가 그려질것입니다.
fig = plt.figure(figsize=(7, 7))
ax = plt.axes(projection='3d') #projection이 차원을 나타낸다.
ax.xaxis.set_tick_params(labelsize=15) #숫자 폰트사이즈
ax.yaxis.set_tick_params(labelsize=15)
ax.zaxis.set_tick_params(labelsize=15)
ax.set_xlabel('$x$', fontsize=20)
ax.set_xlabel('$y$', fontsize=20)
ax.set_xlabel('$z$', fontsize=20)
ax.scatter3D(X, Y, Z, marker='.', color='gray') #3D로 scatter를 그려달라는 뜻
plt.show()
함수의 그래프 방식 표현
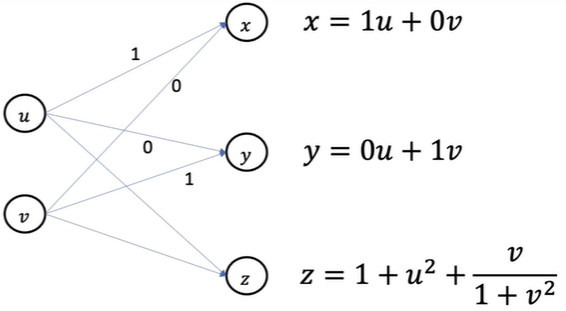
동그라미는 node, 화살표는 edge라고 합니다.
함수의 합성
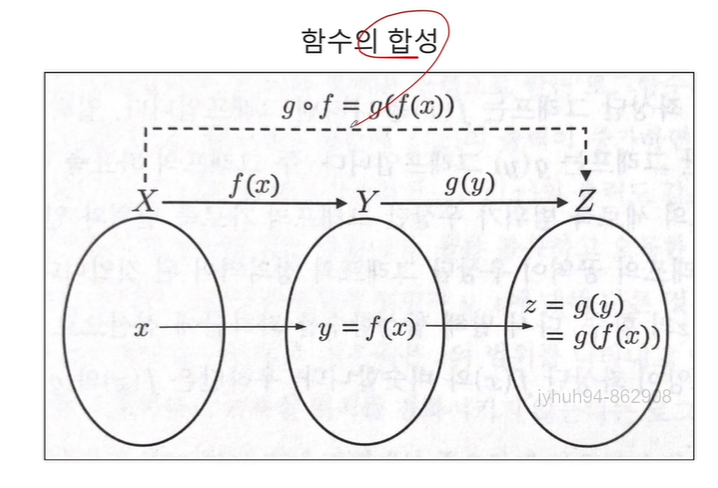
함수를 두번 통과하는것으로 g(f(x))와 같습니다.
함수의 합성 예제
x = np.linspace(-4, 4, 100)
y = x**3 - 15*x + 30 #f(x)
z = np.log(y) #g(y)
두 함수의 표현
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
ax[0].plot(x, y, label='$s^3-15x+30$', color='k')
ax[0].legend(fontsize=18)
ax[1].plot(y, z, label='$\log(y)$', color='k')
ax[1].legend(fontsize=18)
plt.show()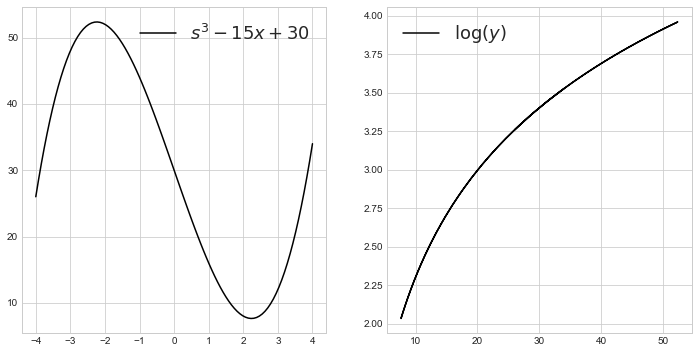
두 그래프의 합성 결과를 보겠습니다.
fig, ax = plt.subplots(1, 2, figsize=(12,6))
ax[0].plot(x, z, '--', label='$\log(f(X))$', color='k')
ax[0].legend(fontsize=18)
ax[1].plot(x, y, label='$x^3-15x+30$', color='k')
ax[1].legend(fontsize=18)
plt.show()
두 그래프를 제대로 비교하기위해 코드를 추가해보겠습니다.
두번째 그래프에 축을 두개로 삼아서 두 그래프를 한번에 비교해보겠습니다.
fig, ax = plt.subplots(1, 2, figsize=(12,6))
ax[0].plot(x, z, '--', label='$\log(f(X))$', color='k')
ax[0].legend(fontsize=18)
ax[1].plot(x, y, label='$x^3-15x+30$', color='k')
ax[1].legend(fontsize=18)
#추가
ax_temp = ax[1].twinx() #x축을 두개 그린다는 뜻입니다.
ax_temp.plot(x, z, '--', label='$\log(f(X))$', color='k')
plt.show()
'머신러닝 > Model Evaluation' 카테고리의 다른 글
| Python Box plot (0) | 2024.04.27 |
|---|---|
| 모델평가_ROC 커브 그리기 (0) | 2024.04.02 |
| 모델평가_ROC와 AUC 개념 (0) | 2024.03.12 |
| 모델평가_모델평가란? (0) | 2024.03.11 |



