최소자승법, OLS란 Ordinary Linear Lease Square의 약자로, 회귀로 문제를 푸는 방법을 해보겠습니다.
그 중에서 수학적으로 많이 사용하는 방법이 OLS입니다.
이 방법에 대해서 알아보겠습니다.
이렇게 생긴 데이터를 하나의 직선으로 만든다고 해봅시다.

총 5개의 데이터를 직선으로 만든다면, y=ax+b 형태를 띌 것입니다. 우리는 x, y를 알고 있으므로 a, b를 찾아야합니다. 어떤 직선이 잘맞는지 모르기 때문에 각 데이터를 넣어야합니다.
1=1a+b
3=2a+b
4=3a+b
6=4a+b
5=5a+b
이 문제를 벡터와 행렬로 표현한다면, 결과적으로 Y = AX라고 표현할 수 있습니다.

y1 = x1*a+b
y2 = x2*a+b
...와 같이 되므로
위에서 얘기한 5가지 식과 동일하게 나타낼 수 있습니다.
우리가 찾고싶은건 X이고 X는 a,b로 이루어져있습니다.
AX=Y인데 여기서 A가 nXn 짜리 정방형 square matrix(정방렬)가 아닙니다. 따라서 역행렬을 양쪽에 곱해서 해결할 수 있는 문제가 아닙니다.
따라서 A의 transfose를 곱합니다.
A는 m*n짜리 행렬이면
A^T는 n*m짜리 행렬입니다.
A^T * A 로 둘을 곱하면 (nXm)(mXn) = (nXn)짜리 행렬이 나옵니다
따라서 양쪽에 A의 transfose를 곱합니다. 이렇게되면 (A^T*A)X = A^T*Y이고 괄호안의 값은 정방렬입니다.
따라서 X = (A^T*A)^-1 * A^T * Y 입니다. *여기서 ^-1은 역행렬을 나타냅니다.

드디어 X를 찾을 수 있습니다. 이것이 최소자승법, OLS을 이용하는 방식입니다.
다시 본래의 문제로 돌아가보겠습니다.


식을 전개해보면 아래와 같이 표현할 수 있고,
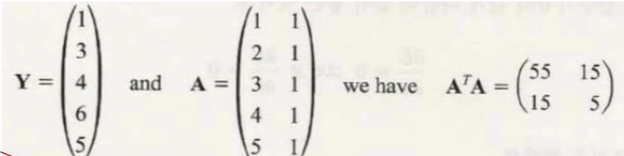

A^T인
(12345
11111) 을 곱해주면 위와같은 결과가 나온다.
최종모델은 y = 1.1x+0.5가 나옵니다.
이 상태에서 모델의 성능을 표현하자면,

E(error)는 현재값에 예측값을 빼서 제곱을 한 값입니다. 원래 에러는 [y-f(x)]^2 에 루트를 씌우기도 하고 평균값을 내기도하는데 여기서는 제곱만 시켰습니다. 실제 참값 1,3,4,6,5와 모델에 1,2,3,4,5를 넣은 값을 빼고 제곱해서 지표를 만들었습니다.
방금 내용을 실습해보겠습니다.
실습
먼저 statsmodels 모듈을 다운로드받습니다.
!pip install statsmodels
그 후 임의의 데이터를 만들어보겠습니다.
import pandas as pd
data = {'x':[1, 2, 3, 4, 5], 'y':[1, 3, 4, 6, 5]}
df = pd.DataFrame(data)
df
이제 가설을 세워보겠습니다.
statsmodels의 formula의 api를 smf라고 하고 여기서 ols를 가져오겠습니다.
import statsmodels.formula.api as smf
lm_model = smf.ols(formula='y ~ x', data=df).fit()
lm은 linear regression model이고
smf에서 제공하는 ols(우리가 지금 배우고있는 최소자승법)
ols에서 이 때의 formula는 y ~ x이고 이건, y ~ x는 y=ax+b라는 뜻입니다.
이제 학습을 완료했으니 params를 확인해보겠습니다.
params를 통해 a, b를 구할 수 있습니다.
lm_model.params
y절편이 0.5, 기울기가 1.1인걸 알 수 있습니다.
그래프를 한번 그려볼까요? 그래프는 seaborn의 lmplot을 사용해서 데이터와 같이 보겠습니다.
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inlineplt.figure(figsize=(10, 7))
sns.lmplot(x='x', y='y', data=df);
plt.xlim([0, 5]) #그래프가 0부터 시작하게 x의 범위를 0부터 5까지로 바꿨습니다.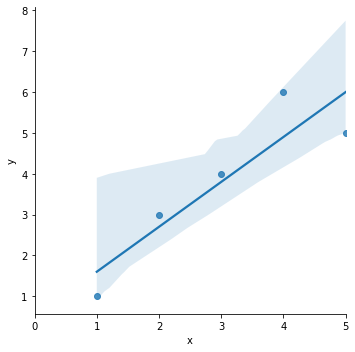
y절편이 0.5가 맞다는걸 보여줍니다.
잔차 평가 residue
- 잔차는 평균이 0인 정규분포를 따르는 것이어야 합니다.
- 잔차는 내 모델과 실제값의 차이로 위 그래프에 의하면 점에서 선 사이의 거리입니다.
- 잔차 평가는 잔차의 평균이 0이고 정규분포를 따르는 지 확인하는 과정이 필요합니다.
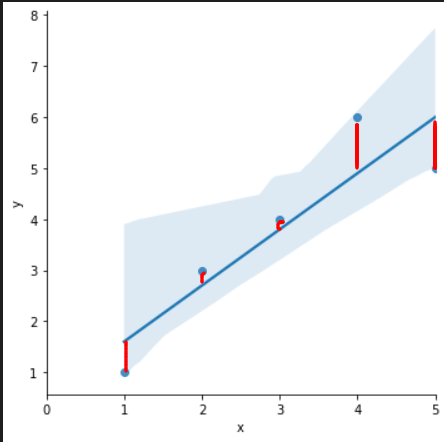
각 데이터별 잔차를 python을 통해 확인해보겠습니다.
resid = lm_model.resud
resid
결정계수 R-Squared

- y_hat은 예측된 값
- 예측 값과 실제값 (y)이 일치하면 결정계수는 1이 된다(즉 결정계수가 높을 수록 좋은 모델)
녹색선이 평균 μ 입니다. 참값이 가지는 평균으로부터의 오차(y- μ)가 분모, 예측값의 평균으로부터의 오차(y_hat- μ)가 분자에 들어가고 각각의 제곱의 합을 나눠준게 결정계수(제곱 상태)입니다.
데이터가 처음부터 평균에 몰려있다면 R-Squared는 좋은 값을 가지게 됩니다. 회귀모델에서 자주 쓰이는 지표이니 기억해두는게 좋습니다. 그러나 머신러닝에서는 예측 성능을 더 중요시 여기긴 합니다.
결정계수를 python을 통해 실습해보겠습니다.
import numpy as np
mu = np.mean(df['y'])
y = df['y']
y_hat = lm_model.predict() #직선상에 있는 값을 가져옵니다.
np.sum( (y_hat-mu)**2 )/np.sum( (y-mu)**2 ) #--> R^2 결정계수가 나옵니다
그런덴 이렇게 복잡하게 구하지않고, python을 통해 구하면
lm_model.rsquared
이렇게 쉽게 구할 수 있습니다.
여기서 주의할 점은 저 R squared값 만으로 높다 낮다를 평가할 순 없습니다. 또 다른 모델을 갖고와서 그 값을 비교해야합니다.
+ 아까 구한 잔차 값을 한번 distplot으로 그려보겠습니다.
sns.distplot(resid, color='black')
나름 정규분포 스럽게 보이긴합니다.
'머신러닝 > Linear Regression' 카테고리의 다른 글
| Cost function - Boston 집값 예측 (0) | 2024.05.05 |
|---|---|
| Cost function과 gradient descent_2 (0) | 2024.05.04 |
| 회귀를 통해 이해하는 Cost function_1 (0) | 2024.05.03 |
| [통계] 회귀 (1) | 2024.05.03 |
| 선형 회귀(Linear Regression) - 회귀 (1) | 2024.04.28 |



